Introduction
Nicholas Hawksmoor (1661–1736) is considered by many to be the leading architect of the late English Baroque. From humble beginnings as a draughtsman in Sir Christopher Wren’s Office of Works, he rose to become Wren’s principal assistant, and his collaborator at St Paul’s Cathedral and Greenwich Hospital. Hawksmoor developed a style quite distinct from that of his mentor. Nowhere is this seen more clearly than at Christ Church, Spitalfields (1714–29), and St Mary Woolnoth (1716–27) in the City of London. These are two of six churches that were designed by Hawksmoor as part of an ambitious project, instigated by an Act of Parliament in 1711, to provide fifty new churches to cater for the rapidly expanding population of London and its suburbs.1 The Hawksmoor churches contain elements of a diverse range of architectural styles, and their towers and spires evoke the Gothic of medieval English cathedrals. Christ Church in particular has the appearance of a ‘classicised’ version of a Gothic cathedral (Figure 1).
The architectural theorists of the Renaissance had been very disparaging about the Gothic style. Writers after Vasari and Serlio associated Gothic architecture with the Germanic tribes who caused the downfall of Roman civilisation.2 This prejudice was waning in early 18th-century Britain, where a gradual rehabilitation of the Gothic style is evidenced by the popularity of the books produced by the architect Batty Langley, lavishly illustrated to encourage builders and craftsmen to adopt Gothic motifs in their work (Langley 1726; Langley and Langley 1747).3 In a number of projects, Hawksmoor imitated the forms and appearance of Gothic architecture, albeit in a plainer and more ‘classicised’ manner. He did this most notably at All Souls College, Oxford (1708–30), and his design for the west gable and towers at Westminster Abbey (1734).4 In this, he may have been following the example of Wren. At the time he first joined Wren’s Office of Works (in 1679 or 1680), Wren was completing Tom Tower at Christ Church College, Oxford (1681–82), designed — against some opposition — in a ‘Gothic’ manner.5 Hawksmoor assisted Sir John Vanbrugh at Castle Howard and at Blenheim Palace, and Vanbrugh’s combination there of classical and medieval elements was probably a further influence (Hart 2008).6 Hawksmoor’s letter of 1734/5 to Joseph Wilcocks, the Dean of Westminster, shows that he considers what he calls ‘the Gothick or Monastick manner’ to be a valid style, since it was the architecture of earlier Christian worship in England.7 Hawksmoor was clearly appreciative of the forms and appearance of Gothic architecture, and able in his own projects to copy and transpose them. The question remains to what extent he was aware of the design procedures that underpinned medieval Gothic design.
Builders since antiquity have used simple whole-number ratios, such as 2:3 and 3:4, to determine the relationships between the different parts of their buildings. In the Middle Ages, builders supplemented these ratios with a set of ‘irrational number’ ratios that were based on simple geometrical shapes. Lon Shelby coined the term ‘constructive geometry’ for these procedures (Shelby 1972; Shelby 1976). The shapes most commonly used were the square and the triangle.8 In his Journal written around 1230, Villard de Honnecourt records the plan of a Cistercian church designed from assembled squares (Barnes 2009: fol. 20r). Shelby provides a commentary on the pamphlet of 1486 written by master mason Mathes Roriczer that demonstrates the procedure of rotating inscribed squares to generate the proportions needed to construct a pinnacle (Shelby 1976). This was design ad quadratum.9 Design based on triangular construction was also common. The elevation scheme at Notre-Dame in Paris was designed around an equilateral triangle (Sandron and Tallon 2013), as were the elevations at the cathedrals of Bourges (Bork 2014), Beauvais (Murray 2015), Strasbourg and Milan (Bork 2011). In a celebrated paper, James Ackerman describes the debate at Milan Cathedral over whether to use a triangle or a square in planning the elevation scheme (Ackerman 1949). Particular ratios were developed from these geometric shapes: Nicola Coldstream illustrates how the ratio 1:√2 was derived from the side and diagonal of a square of unit length, while the ratio 1:√3 was derived from the height of an equilateral triangle (Coldstream 2002: 68). These geometrically derived ratios are not whole numbers; the value of √2 is 1.414 (to three decimal places), and √3 is 1.732.
Medieval masons did not have to calculate these irrational numbers, since they used a set of whole-number ratios that approximated those relationships.10 It is likely that they inherited these geometrically derived (hereafter ‘geometric’) ratios, and their whole-number approximations, from builders and land surveyors of the late Roman era (Kidson 1990; Kidson 2008). Mark Wilson Jones has investigated the design proportions in a wide sample of Roman buildings, and concludes that they were mostly simple whole-number ratios, but with geometric ratios, most commonly √2 and √3, in ‘a substantial minority of cases’ (Wilson Jones 2003: 87). Numerous studies in recent years have found ratios based on √2 in Roman buildings (for example, Fletcher 2019; Hallier 1990), and a smaller number suggest the use of √3 (see Jacobson 1990; Kalayan 1971). However, these are recent studies, based on modern surveying techniques and conducted onsite. It is unlikely that Hawksmoor, who did not visit Rome, would have been able to deduce these geometric ratios from the books and illustrations that were available to him — for instance, the several editions of Palladio’s Quattro Libri in his own library. He is more likely to have associated geometric ratios with the Gothic style. As a young man, he studied and drew Bath Abbey; later in his career, he oversaw the restoration of Beverley Minster and Westminster Abbey; and in a letter of 1735 to Dean Wilcocks he shows a detailed knowledge of Durham Cathedral, York Minster and the medieval churches of Lincoln, Lichfield and Ripon (Downes 1959: 258–60). Furthermore, his association of the Gothic style with geometric ratios would likely have been reinforced by his contact with, or direct involvement in, Freemasonry, as discussed below.
The presence of geometric ratios in Renaissance architecture is vigorously debated. Palladio mentions the ratio 1:√2 as one of his preferred design ratios (Palladio 1997: 57), as do Serlio (Serlio 1996: 30) and Alberti (Alberti 1988: 305–9). Cesare Cesariano added an illustration of the design scheme ad triangulum at Milan Cathedral to his 1521 edition of Vitruvius (Wittkower 1974: 24–26). Despite this, Rudolph Wittkower, in his highly influential study Architectural Principles in the Age of Humanism, suggests that ‘it is probably right to say that rarely did Palladio or any other Renaissance architect use irrational proportions in practice’ (Wittkower 1962: 108). Wittkower’s view has been challenged in recent times. Matthew Cohen has found that Brunelleschi made extensive use of the ratio 1:√2 in the basilicas of San Lorenzo and Santo Spirito in Florence (Cohen 2013). Branko Mitrović has found that the ratios 1:√2 and 1:√3 occur several times in Palladio’s villas, as measured by Bertotti Scamozzi (Mitrović 2004: esp.190–197). In a recent survey of Palladio’s Church of the Redentore, I found several instances where the ratios 1:√2 and 1:√3 are used for significant proportional relationships in the church interior (Hales 2023). I had previously found these same ratios present in Francesco Borromini’s early Baroque church of San Carlino in Rome (Hales 2020). Despite this, it would seem (from the survey evidence currently available) that the use of geometric ratios during the Renaissance and the Baroque was the exception, rather than the rule.11 Again, Hawksmoor is more likely to have associated geometric ratios with the Middle Ages than with the Renaissance.
This present study aims to address the extent to which Hawksmoor understood the design formulas underpinning the forms and appearances of the Gothic style, and investigates whether he adopted these procedures in his own churches. The dimensions of two of Hawksmoor’s most celebrated London churches — Christ Church, Spitalfields, and St Mary Woolnoth — were measured and their design proportions calculated. Previous attempts to analyse the design of the two churches are insightful (Downes 1959; Hopkins 2015), but they have the disadvantage of being based on only the church plans — the horizontal dimensions — rather than on detailed survey measurements of both plan and elevation (i.e., both horizontal and vertical dimensions).
Method
The dimensions of both churches were initially estimated from an examination of survey drawings by contemporary architects. For Christ Church, these were the survey drawings published by London County Council (Sheppard 1957), as well as the drawings by the architects Whitfield and Partners, who oversaw the church restoration in its final phases between 1996 and 2004. For St Mary Woolnoth, drawings from 2021 by Roger Mears Architects were examined. I then made a number of decisions about what constituted the most significant dimensions in both churches: those most important either structurally — the length of nave, the height of ceiling, etc. — or visually — the heights to the top edge of the wall cornice or the bottom edge of the architrave, the heights to the crown of an arch or the head soffit over a window. I made decisions about where the measurements should be taken: measuring to the interior surfaces of walls rather than their exteriors (except where otherwise noted below), and measuring to the inner and outer edges of column pedestals, rather than from centre to centre of the columns.12 The altars in all of Hawksmoor’s churches are situated three steps up from the nave.13 Significant proportional relationships emerged when all the vertical dimensions were calculated from the nave floor level. I then reviewed these decisions during the later phase of direct measurement in the churches. The dimensions that seemed the most significant were measured on the survey drawings, and the proportional relationships between these measurements were calculated. Based on the estimates derived from this paper investigation, I then conducted detailed surveys of the two churches between January 2022 and December 2023.
These onsite measurements were laser-assisted manual surveys. The hand-held Leica Disto D510 laser measure was used to take a large set of single-point measurements. The advantage of the laser measure lies in its accuracy over long distances and the way it allows for height and angled measurements that would otherwise be impractical to achieve. The majority of the laser measurements were taken horizontally or vertically, for which the Leica D510 has an accuracy of plus or minus 1 mm, up to a distance of 200 m. A few height measurements were taken as angled measurements, for which the laser measure is somewhat less accurate. Small distances were measured with a standard steel tape measure. Erring on the side of caution, the measurements quoted in this study can be considered accurate to 0.05 ft, or half an inch. Single-point laser measurement provides less information than 3D laser scanning. To compensate for this, a considerable number of single point measurements were taken (some 900 measurements across the two churches). Each structural feature discussed in the text (and listed in Tables 1 and 2 below) was measured from ten different positions. For some principal dimensions, such as the nave width and the ceiling height, fifteen or more measurements were taken. This allowed for irregularities and out-of-square alignments, since the modal (most commonly occurring) value for each set of readings was taken as the ‘correct’ figure. The measurements were taken in (British) feet, rather than metres.14 Hawksmoor often labelled his drawings in feet and inches, but it was decided to quote the dimensions in this study in decimal fractions of feet, to allow for a more transparent calculation of the ratios between dimensions (0.1 ft is 1.2 inches). Proportional relationships were calculated between the significant dimensions that had been measured in the survey, and these were compared with the design ratios common in medieval Gothic building. In these calculations, the percentage discrepancies between measured ratios and design ratios were rounded up or down to the nearest 0.1%.
The proportional relationships at Christ Church, Spitalfields that match Gothic design ratios, showing the amount of discrepancy between them; the dimensions are rounded to the nearest 0.05 feet, and the discrepancy percentages are rounded to the nearest 0.1%. The asterisk marks the one match that falls outside the estimated range of construction tolerance for the church.
| DIMENSION A (feet) | DIMENSION B (feet) | RATIO | RATIO: EXACT AMOUNT | DISCREPANCY (feet) | DISCREPANCY (%) |
| CHURCH INTERIOR | |||||
| Nave width between pilasters (64.95) | Total church interior length (131.10) | 1:2 | 129.90 | 1.20 | 0.9 |
| Nave width between pilasters (64.95) | Length of nave and chancel (113.00) | 1:√3 | 112.50 | 0.50 | 0.4 |
| Nave width between pilasters (64.95) | Chancel width (32.75) | 2:1 | 32.50 | 0.25 | 0.8 |
| Diagonal of nave length rectangle (114.90) | Length of nave and chancel (113.00) | 1:1 | 114.90 | 1.90 | 1.7* |
| Diagonal of nave and chancel rectangle (130.35) | Total church interior length (131.10) | 1:1 | 130.35 | 0.75 | 0.6 |
| Diagonal of interior length rectangle (146.30) | Length to exterior west wall of church (146.35) | 1:1 | 146.30 | 0.05 | 0.0 |
| Width between outer edges of cross-shaped pedestals (45.45) | Nave width between pilasters (64.95) | 1:√2 | 64.30 | 0.65 | 1.0 |
| Length between outer edges of cross-shaped pedestals (51.05) | Length between inner edges of square pedestals (71.50) | 1:√2 | 72.20 | 0.70 | 1.0 |
| Diagonal of cross-pedestal rectangle (68.35) | Length to west wall of narthex (138.40) | 1:2 | 136.70 | 1.70 | 1.2 |
| Length between outer edges of square pedestals (78.55) | Total church interior length (131.10) | 3:5 | 130.90 | 0.20 | 0.1 |
| Height of nave ceiling (56.35) | Length of nave and chancel (113.00) | 1:2 | 112.70 | 0.30 | 0.3 |
| Triangle on nave width between pilasters (64.95) | Height of nave ceiling (56.35) | Triangle 1:√3/2 |
56.25 | 0.10 | 0.2 |
| Height of main order cornice (37.40) | Nave width between pilasters (64.95) | 1:√3 | 64.80 | 0.15 | 0.3 |
| Height of upper cornice (46.15) | Nave width between pilasters (64.95) | 1:√2 | 65.25 | 0.30 | 0.5 |
| Nave width between pilasters (64.95) | Height of arcade arches (43.15) | 3:2 | 43.30 | 0.15 | 0.3 |
| Height to top of side aisle windows (9.70) | Height to top of long windows (24.40) | 2:5 | 24.25 | 0.15 | 0.6 |
| Height to top of long windows (24.40) | Height to top of round windows (36.55) | 2:3 | 36.60 | 0.05 | 0.1 |
| EAST FAÇADE | |||||
| Triangle on east façade width (75.90) | Height to apex of pediment (65.90) | Triangle 1:√3/2 |
65.75 | 0.15 | 0.3 |
The proportional relationships at St Mary Woolnoth that match Gothic design ratios, showing the amount of discrepancy between them; the dimensions are rounded to the nearest 0.05 feet, and the discrepancy percentages are rounded to the nearest 0.1%.
| DIMENSION A (feet) | DIMENSION B (feet) | RATIO | RATIO: EXACT AMOUNT | DISCREPANCY (feet) | DISCREPANCY (%) |
| Nave width between side walls (51.90) | Nave length (52.00) | 1:1 | 51.90 | 0.10 | 0.2 |
| Nave width between side pilasters (49.65) | Height of nave ceiling (49.15) | 1:1 | 49.65 | 0.50 | 1.0 |
| Width of narthex (28.20) | Length of nave and altar recess (57.05) | 1:2 | 56.40 | 0.65 | 1.1 |
| Nave width between side pilasters (49.65) | Total interior length of church (67.05) | 3:4 | 66.20 | 0.85 | 1.3 |
| Width between outer edges of colonnade pedestals (35.30) | Nave width between side pilasters (49.65) | 1:√2 | 49.90 | 0.25 | 0.5 |
| Width between inner edges of colonnade pedestals (28.80) | Nave width between side pilasters (49.65) | 1:√3 | 49.90 | 0.25 | 0.5 |
| Diagonal of colonnade rectangle (49.60) | Nave width between side pilasters (49.65) | 1:1 | 49.60 | 0.05 | 0.1 |
| Length of nave and altar recess (57.05) | Height of nave ceiling (49.15) | Triangle 1:√3/2 |
49.40 | 0.25 | 0.5 |
| Nave width between side pilasters (49.65) | Height to base of lunette window keystones (43.45) | Triangle 1:√3/2 |
43.00 | 0.45 | 1.0 |
| Height of main cornice (32.40) | Height to top of lunette window keystones (46.05) | 1:√2 | 45.80 | 0.25 | 0.5 |
| Height of main architrave (27.85) | Height to top of lunette window keystones (46.05) | 3:5 | 46.40 | 0.35 | 0.8 |
| Height to top of south aisle windows (26.60) | Height to top of lunette window keystones (46.05) | 1:√3 | 46.05 | 0.00 | 0.0 |
| Height of main cornice (32.40) | Height of nave ceiling (49.15) | 2:3 | 48.60 | 0.55 | 1.1 |
| Height of side aisle ceilings (31.20) | Nave length (52.00) | 3:5 | 52.00 | 0.00 | 0.0 |
| Height of side aisle ceilings (31.20) | Nave width between side walls (51.90) | 3:5 | 52.00 | 0.10 | 0.2 |
| Height of chancel arch (26.00) | Height of main cornice (32.40) | 4:5 | 32.50 | 0.10 | 0.3 |
When considering the relationship between design ratios and structural proportions, the key question is the degree of correlation or match that either proves or disproves the case. Among architectural historians, opinion differs on this issue, while it is generally agreed that some allowance should be made for ‘construction tolerance’ (that is to say, inaccuracies or building errors that inevitably occur during a construction project). The type of research described in this present study, comparing design ratios and built structures, is more common in the examination of medieval churches. Here the ‘rule of thumb’ is that a discrepancy of anything up to 1.0% can be considered a valid match. For example, Nigel Hiscock, discussing measurements taken at Durham Cathedral, describes ‘allowing for discrepancies of less than 1%, which may reasonably be attributed to building errors’ (Hiscock 2000: 236). Marie-Therese Zenner discusses the ratios between the vault heights at the church of Sainte-Etienne in Nevers, and considers an acceptable degree of tolerance as being anything less than 1% (Zenner 2002: 28). Stephen Murray discusses the relationship between the width and height in the choir of Beauvais Cathedral. He describes a match with a discrepancy of 1.5% as unconvincing, while he considers a related match with a discrepancy of 0.9% to be valid evidence to reinforce his hypothesis about the design (Murray 2014: 5–13).
More evidence is available from the buildings of Christ Church and St Mary Woolnoth themselves. The large number of measurements that were taken made it possible to calculate the level of construction tolerance in the two churches. As will be described more fully below, the length of the nave at Christ Church is 94.80 ft on the north side and 94.95 ft on the south side. This is a difference of 0.15 ft, which is 0.15% of 94.80 ft. The nave width between the side wall pilasters is 0.20 ft narrower in the middle than at the ends, in a distance of 64.95 ft. This amounts to a discrepancy of 0.3%. At St Mary Woolnoth, the nave is 0.15 ft longer along the north wall than on the south wall, over a distance of 52.00 ft, which is a construction discrepancy of 0.3%. The height of three of the south aisle windows is 26.60 ft, while that of a fourth window is 26.65 ft. This is a discrepancy of 0.2%. These four instances suggest that, as a conservative estimate, plus or minus 0.2% could be considered the benchmark level of construction tolerance (that is, building inaccuracy) across the two churches. Furthermore, this study concerns a series of proportional relationships, each between two structural dimensions. The construction error can affect both dimensions, and so this potential error is magnified in the relationship between them. For example, if Dimension A is built 0.2% shorter than the architect intended, and Dimension B is built 0.2% longer than intended, then the proportional ratio between them will be 0.4% larger than the design ratio intended by the architect. This is so regardless of the particular ratio between them (whether it is 1:2, 1:√2, 1:√3 and so on). It follows from this that where a proportional relationship varies from a design ratio by (for example) 1.4%, then up to 0.4% of this discrepancy can be the result of construction error. The fundamental mismatch with the intended design ratio is possibly only 1.0%. Taking this into account, as well as the level of construction tolerance (plus or minus 0.2%) across the two churches, then any match with a discrepancy less than 1.4% seems worthy of consideration. This may helpfully inform the detailed description that follows of the proportional relationships that were found in the surveys at Christ Church and St Mary Woolnoth.
Christ Church, Spitalfields: Classic and Gothic
Hawksmoor and Wren had a considerable interest in the architectural forms of antiquity, and of the early Christian church. They shared this interest with an influential group of Anglican clergy, who were keen to develop what Owen Hopkins terms ‘a parallel history of Christianity that was, vitally, untainted by Rome and popery’ (Hopkins 2015: 80).15 Wren, and Hawksmoor after him, adopted the three-aisle basilica plan of the early Christian churches, based on the Basilica of Maxentius in the Roman Forum, which was completed by Constantine after his conversion to Christianity (Du Prey 2000; Hart 2002: 52–55). This can be seen at Christ Church, Spitalfields. The nave is a large auditorium, which reflects the emphasis in Protestant theology on preaching and readings from the Bible. Wide wooden galleries to north and south divide the church interior into the three-aisle basilica plan, and there is a further gallery at the west end around the organ.16 Christ Church is significantly taller than Hawksmoor’s previous churches, having a clerestory above the nave. Free-standing Composite columns, mounted on tall pedestals, support the large and imposing main order entablature, which is broken into lateral sections spanning the side galleries.17 At the east end, the main entablature is suspended over the chancel. The giant columns form an arcade down each side of the nave, supporting and then rising above the side galleries (Figure 2). They culminate in a series of high arches, behind which barrel vaults form bays over the side galleries. The three central vaults on each side of the nave are coffered, a visual reference to the Basilica of Maxentius. Pilasters set against the side walls add to the vertical emphasis in the nave. They are significant both structurally and visually, since they frame the three tiers of windows below the clerestory, and they support from the rear the main entablature over the galleries (Figure 3).
Christ Church. The nave with the south arcade and the coffered vaults, showing significant dimensions marked in feet. The square and cross-shaped (centre left) column pedestals can be seen, and the side wall pilasters supporting the broken entablature from the rear. Photo: Jonathan Hales, 2022.
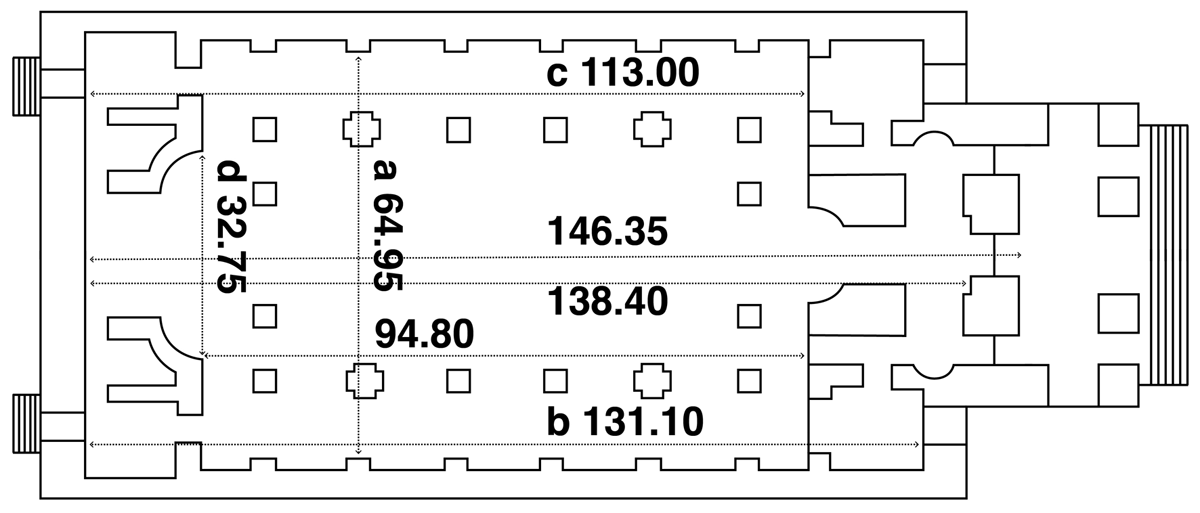
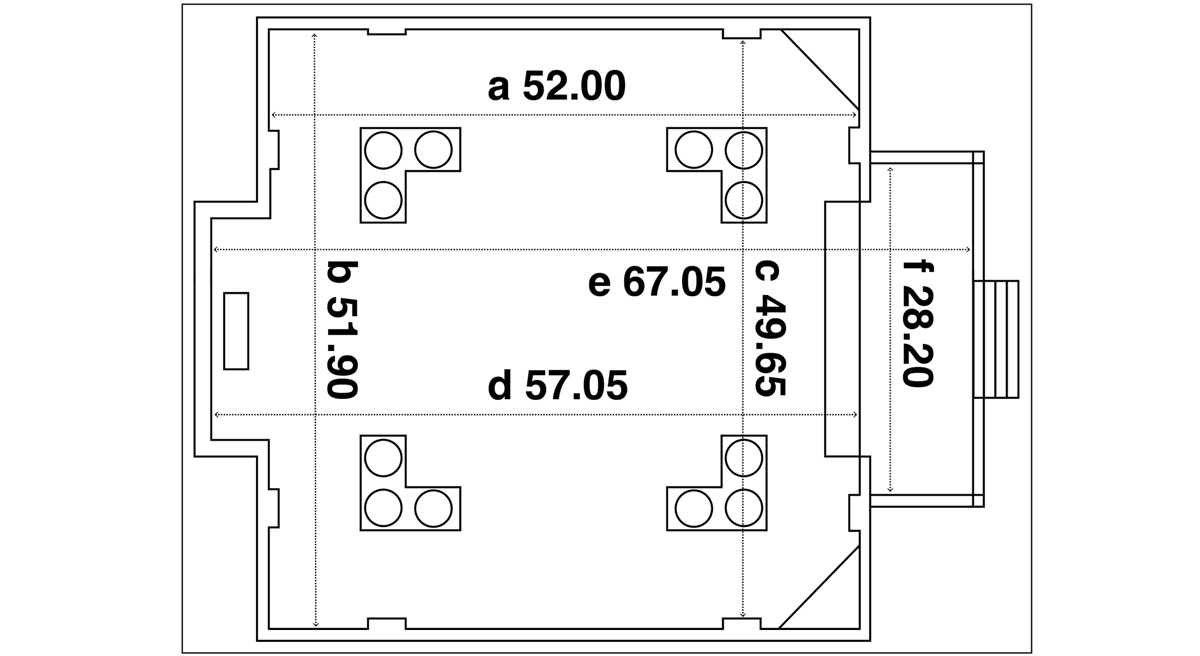
An examination of the most significant dimensions in the church interior reveals a set of proportional relationships that were presumably deliberate choices in the overall design scheme. The length of the nave, from the east walls either side of the chancel to the west walls either side of the nave entrance, is 94.80 ft on the north side and 94.95 ft on the south side (a significant difference of some two inches, as discussed above). The combined length of the nave and chancel, from the east wall behind the altar to the nave’s west walls, is 113.00 ft. The total interior length of the church, from the east wall behind the altar to the west walls of the front vestibules, is 131.10 ft (see the church plan in Figure 4). The nave of the church is impressively wide. Measured as the distance between the pedestals of the side wall pilasters, the nave width is 64.95 ft at both ends of the nave (but 64.75 ft in the middle). This width (64.95 ft) seems to be a key and repeated element in the design scheme at Christ Church. The ratio of the nave width to the total interior length of the church (131.10 ft) is 1:2, with a discrepancy of 0.9%. The ratio of the nave width to the combined length of the nave and chancel (113.00 ft) is 1:√3, with a discrepancy of just 0.4%. Finally, the ratio of the nave width to the width across the west end of the chancel (32.75 ft) is 2:1, with a discrepancy of 0.8%.
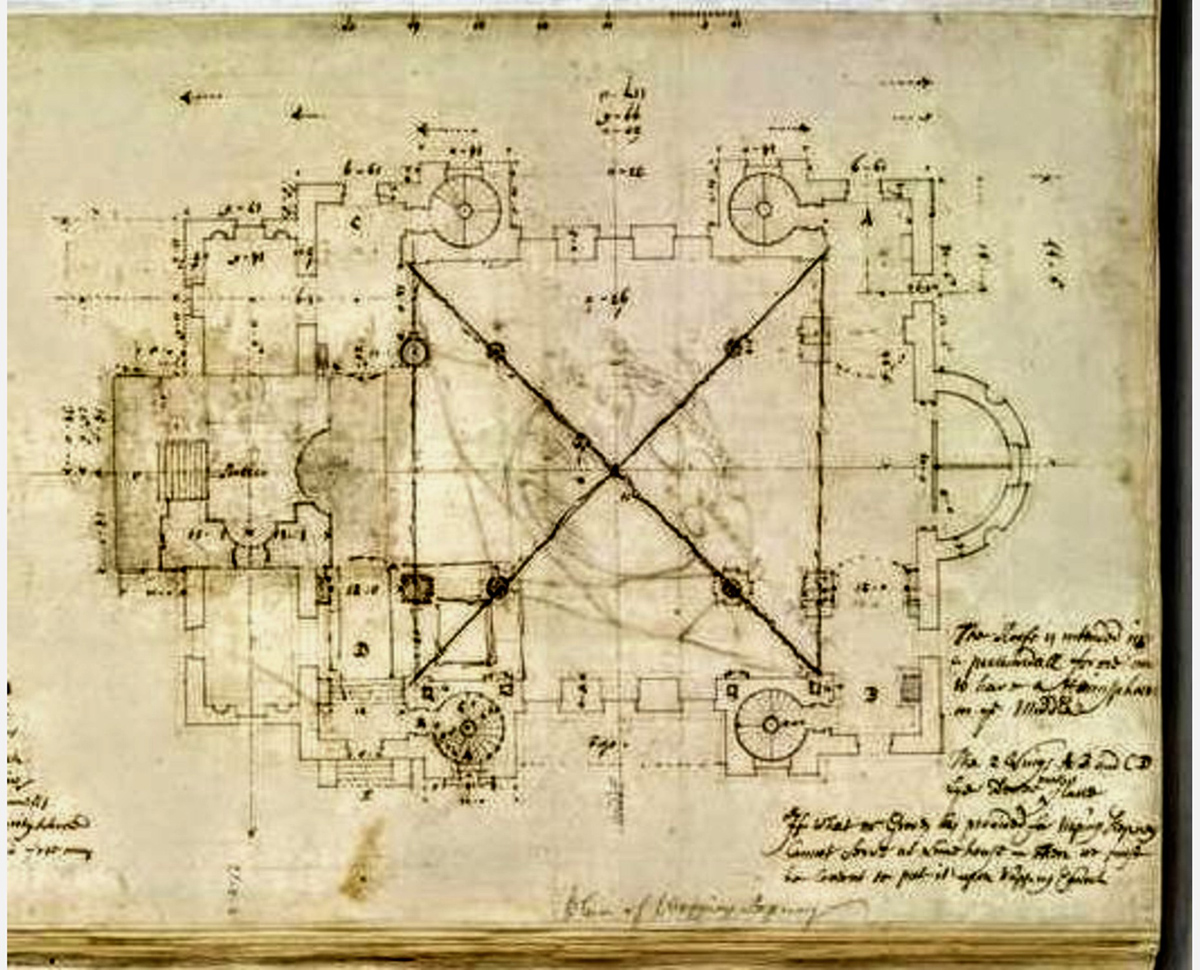
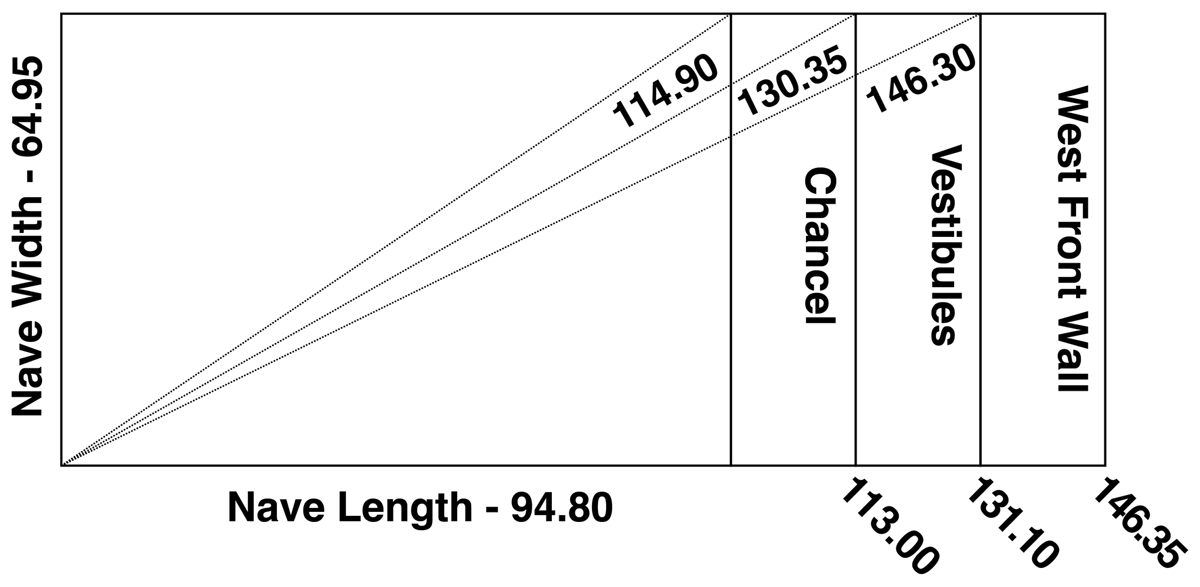
Hawksmoor’s drawing for his contemporaneous church of St George-in-the-East (1714–29) shows the church plan on which he has superimposed the diagonals of the nave, with a heavy emphasis (Figure 5). This suggests that the diagonals were significant in his thinking about the design. The nave at Christ Church is a rectangle 94.80 ft long (north side) and 64.95 ft wide (between side pilasters). The diagonal of this rectangle is 114.90 ft in length, which is close to the combined length of the nave and chancel (113.00 ft). There is a rather large discrepancy here of 1.7%. The combined length of nave and chancel makes a longer rectangle with the nave width, and here the diagonal is 130.35 feet. This is close to the total interior length of the church (131.10 ft), with a discrepancy of only 0.6%. The rectangle formed by the nave width and the total interior length has a diagonal of 146.30 ft, which is very close to the distance between the east wall behind the altar and the exterior west wall of the church, under the portico (146.35 ft). These rectangular constructions are illustrated in Figure 6 (I found a similar design scheme in my recent survey at Hawksmoor’s church of St Anne in Limehouse).18
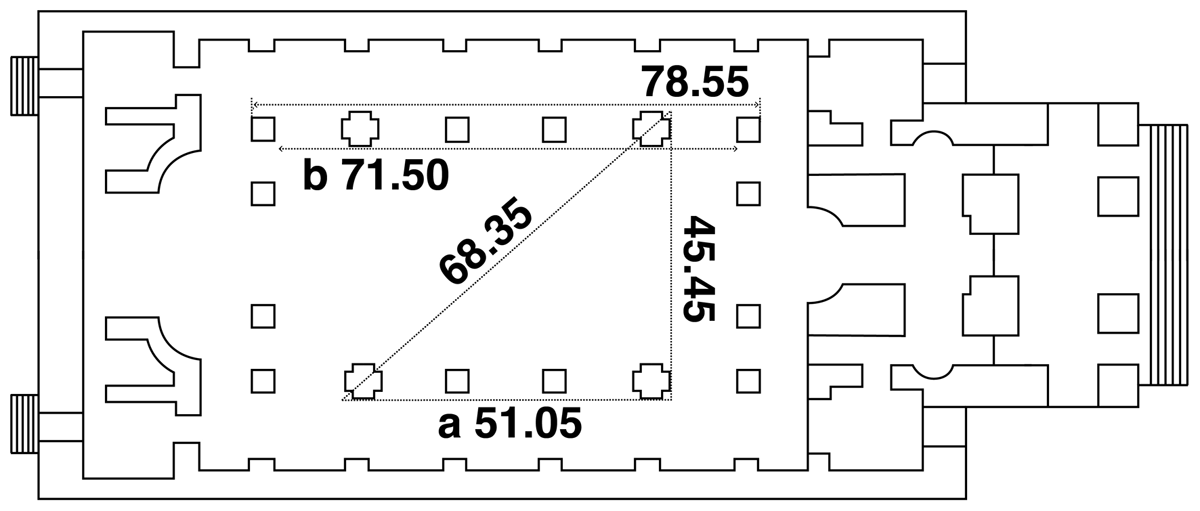
The positioning of the pedestals that support the giant columns in the nave arcade reveals some interesting geometrical relationships. Four cross-shaped pedestals form a rough square within the rectangle defined by the (square-shaped) outer pedestals (Figure 7). The distance across the nave between the outer edges of the cross pedestals is 45.45 ft. The ratio of this distance to the nave width between side pilasters is 1:√2, with a discrepancy of 1.0%. The distance along the length of the nave between the outer edges of the cross pedestals is 51.05 feet. The ratio of this length to the distance between the inner edges of the square pedestals at each end of the nave (71.50 ft) is 1:√2. The discrepancy here is again 1.0%. If an imaginary rectangle were to be constructed, with a length of 51.05 ft and a width of 45.45 ft, then the diagonal of the rectangle would be 68.35 feet. The ratio of this diagonal to the length from the east wall behind the altar to the internal west wall of the entrance narthex (138.40 ft) is 1:2 (see Figure 4). The discrepancy here is 1.2%. Finally, the length between the outer edges of the square pedestals is 78.55 ft. The ratio of this length to the interior length of the church to the vestibule walls (131.10 ft), is 3:5. The discrepancy here is only 0.1%.
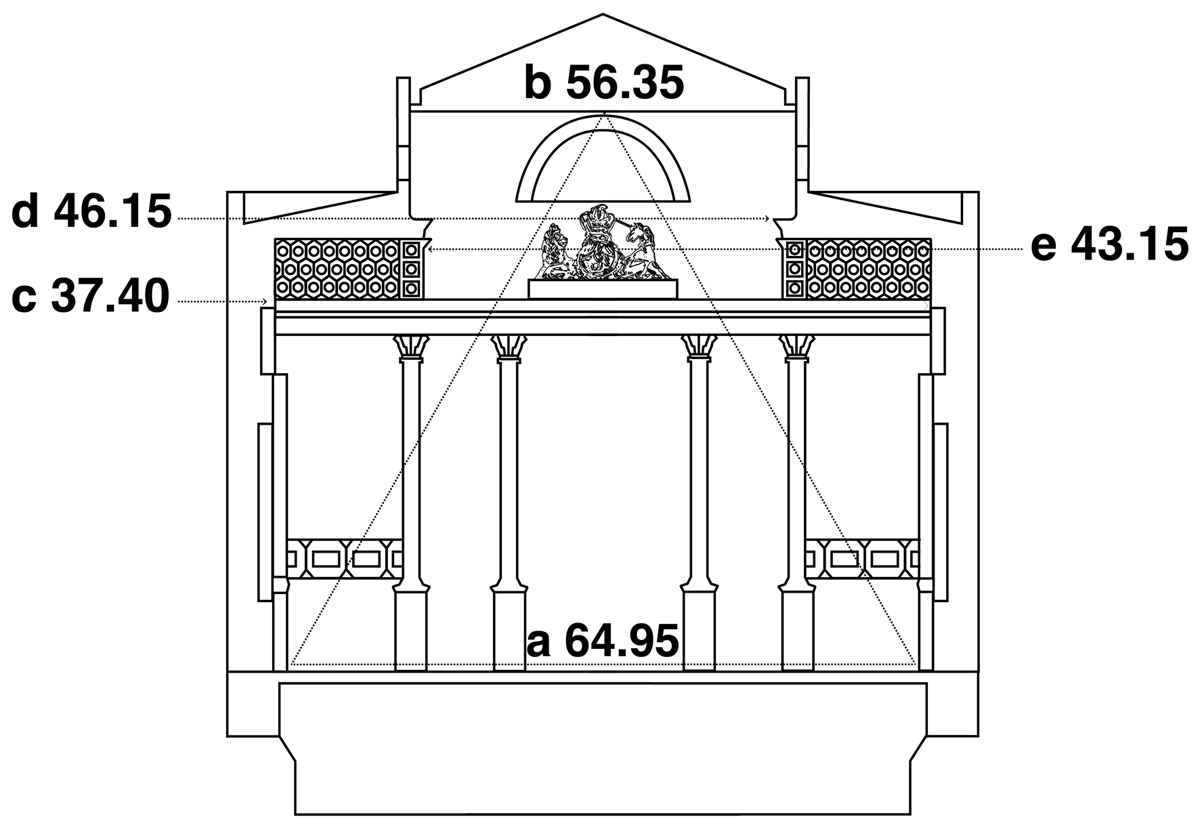
Significant proportional relationships can also be found in the vertical dimensions of the church. The height of the nave ceiling from the nave floor is generally 56.35 ft (although the ceiling has sagged, up to an inch in the centre). This makes the ratio 1:2 with the combined length of nave and chancel, with a discrepancy of only 0.3%. If an imaginary equilateral triangle were to be constructed on the nave width between the side pilasters, with its base at floor level, then the height of the triangle can be calculated as half the width, multiplied by √3. This height matches the height of the nave ceiling, with a discrepancy of just an inch (0.2%). This could be an instance of Hawksmoor emulating medieval design ad triangulum. The nave width between pilasters, when divided by √3, matches the height to the top of the main order cornice (37.40 ft), with a discrepancy of 0.3%. The width, when divided by √2, matches the height of the upper cornice (46.15 ft), with a discrepancy of 0.5%. The upper cornice marks the transition from the nave to the clerestory, and so forms a significant visual division in the elevation (as does the cornice of the main order). The ratio of the nave width to the height of the arches in the nave arcade, measured to their soffit (43.15 ft), is 3:2. There is a discrepancy here of 0.3%. In this way, a notable sequence of whole-number and geometric ratios seems to have been developed from the nave width between side pilasters. These proportional relationships are illustrated in Figure 8.
Proportional relationships also exist between the several tiers of windows in the nave (Figure 9). The height to the top of the side aisle windows is 9.70 ft. The height to the top of the long windows over the galleries is 24.40 ft, and the height of the round windows above them is 36.55 ft. The ratio of the height of the side aisle windows to the height of the long windows is 2:5 (to 0.6%). The ratio of the height of the long windows to the height of the round windows is 2:3 (to 0.1%). The design ratios found in the church interior can also be found on the exterior. The east façade is less impressive visually than the west end, but it has its own beauty. The central section features the large Serlian east window, with a lunette window above. There is a broken pediment over the clerestory. The level of the nave floor is indicated by the bottom of the side doors and the string course that runs between them (Figure 10). The width of the eastern façade at nave floor level is 75.90 ft (some nine feet wider than the interior width of the nave, measured between the side walls, which is 66.55 ft). If an imaginary equilateral triangle were to be constructed on the façade width at nave floor level, then the top of the triangle would match the apex of the pediment cornice (65.90 ft), to within two inches, or 0.3% (Figure 11).
The dimensions and proportional relationships found in the survey at Christ Church are summarised in Table 1 below. Reading the table from left to right, the dimensions measured in the church are shown in columns one and two, with the matching design ratio in column three. Column four displays the magnitude that would be an exact match with the ratio, and column five displays the discrepancy (in feet) between this amount and Dimension B. Column six displays the amount of discrepancy as a percentage of Dimension B. The first line of the table can be taken as an example. The proportional relationship between the nave width between pilasters (64.95 ft) and the length of total church interior (131.10 ft) comes close to the ratio 1:2. For an exact match with the ratio, the church length would need to be 129.90 ft, rather than 131.10 ft. The amount of discrepancy is 1.20 ft. This discrepancy, as a percentage of Dimension B, the church interior length, is 0.9%.
The series of proportional ratios summarised above makes it possible to reconstruct a sequence of steps by which Hawksmoor may have generated his design for the church. The initial decision may have been the total interior length of the church, from the east wall to the vestibule west wall (131.10 ft). This dimension could have generated the nave width between side wall pilasters (2:1), which could then have given the length of nave and chancel (1:√3), the width of the chancel (2:1) and the position of the cross pedestals in the arcade (√2:1). Rectangular construction using the nave width and the length of nave and chancel could have given the total interior length (again), and the length to the exterior west wall. In medieval design, horizontal dimensions in the church plan were generally used to generate the vertical dimensions of the elevation (Coldstream 2002: 66). The nave width between pilasters could have generated the height of the nave ceiling (by triangulation), as well as the height of the main order cornice (√3:1), the height of the upper cornice (√2:1) and the height of the arcade arches (3:2). The height of the long windows in the nave, once decided, could have given the heights of the side aisle windows below (5:2) and the round windows above (2:3). On the east façade, the façade width could have generated the height to the top of the pediment, by triangulation.
St Mary Woolnoth: Geometry and Freemasonry
St Mary Woolnoth in the City of London was built on the pre-existing site of a dilapidated medieval church. Despite its relatively small size, the exterior of the church is monumental in appearance, and somewhat severe (Figure 12). The church interior is a complete contrast (Figure 13). The clerestory has large lunette windows on each of its four sides, and in most weathers the church is flooded with light. The clerestory is high, an arrangement that may have been inspired by Palladio’s illustration of an Egyptian Hall in the Quattro Libri (Palladio 1997: 118). This is even more evident now, since the north and south galleries were removed in 1876. Vaughan Hart has described how masonic iconography can be found throughout St Mary Woolnoth (Hart 2002: 93–98). The rehabilitation of Gothic architecture that occurred in early 18th-century Britain coincided with the rise of Freemasonry, with its celebration of medieval masonic practice. At this time, Freemasonry represented a less sectarian approach to religion and a meeting place for influential people with different political affiliations. Several members of the Commission for Fifty New Churches were Freemasons, including Nathaniel Blackerby, the treasurer. Blackerby’s friend, Batty Langley, was a noted Freemason. Blackerby married Hawksmoor’s daughter, Elizabeth (his only child), in 1735 (Hart 2002: 99). Hawksmoor was assisted in several of the drawings for St Mary Woolnoth by the other Surveyor for the Commission, John James (Downes 1959: 190–91). James, who may have contributed some ideas to the design, was also a Freemason. There is some evidence that Hawksmoor himself became a Freemason sometime before 1730, although like Wren (also thought to have been a mason) he never declared this himself (Hart 2002: 98).19 At St Mary Woolnoth, masonic imagery appears, for example, in the reredos, whose twisted wooden columns allude to the twisted pillars in Solomon’s Temple. Cherubim, which perhaps refer to those on the Ark of the Covenant, appear on the reredos, and on the main entablature above it (Figure 14). The prominent lunette windows in the clerestory feature the masonic Rising Sun motif. Furthermore, the nave, with the clerestory, forms a cube; the cube was again significant in masonic lore since the Temple of Solomon was thought to be cubic in form.
St Mary Woolnoth, the nave looking towards the east end, showing the height in feet of significant features. Masonic imagery is evident in the cherubim on the main entablature below the Royal Arms, and in the glazing bars of the lunette window that evoke the rays of the rising sun. Photo: Jonathan Hales, 2022.
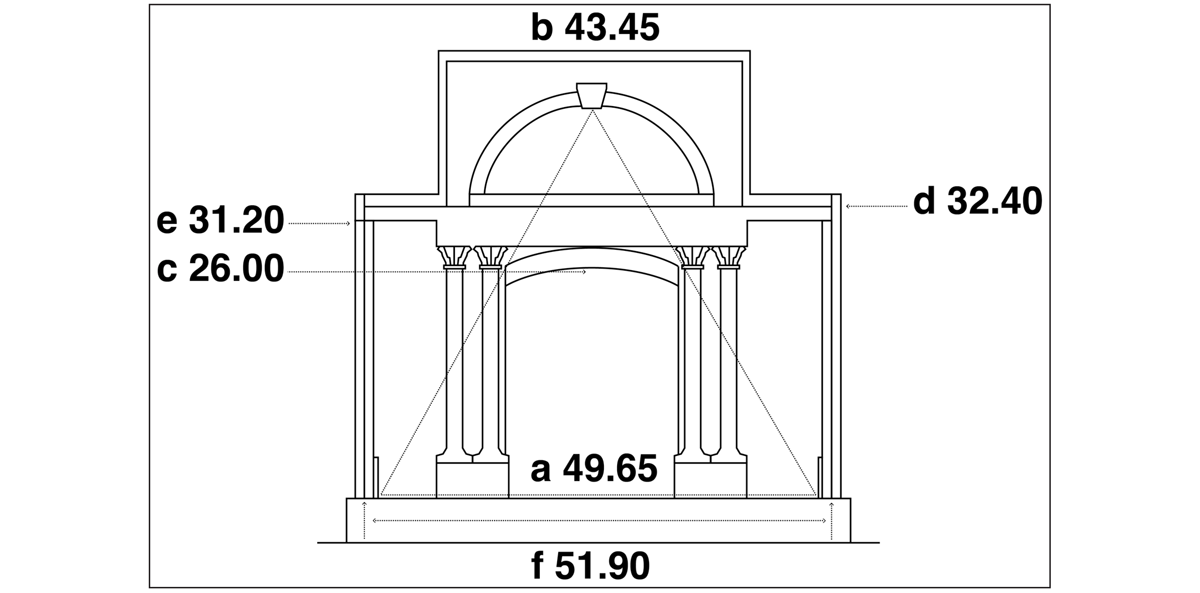
The church nave is square in plan (Figure 15). St Mary Woolnoth has a shallow altar recess (5.05 ft) at the east end, rather than a fully developed chancel. The nave width, measured between the side walls, is 51.90 ft. The nave length, measured from the east walls on either side of the altar recess to the west walls on either side of the nave entrance, is 52.00 ft on the south side (52.15 ft on the north). The nave length (as 52.00 ft) is thus a close match with the width between the side walls. The height of the nave ceiling from the nave floor is generally 49.15 ft (although, as at Christ Church, the ceiling has sagged slightly towards the middle). The ceiling height is thus a poor match with the width between the side walls, but a much closer match with the width measured (as at Christ Church) between the side wall pilasters (49.65 ft). Here the discrepancy is 1.0%, or six inches. Thus the interior space of the nave is nearly a cube. David Harrison writes about the significance of the number seven in masonic lore (Harrison 2009: 54). It may not be a coincidence that the dimensions of the nave width and height are (roughly) 49 feet, since 49 is seven times seven. The ratio of the width of the narthex (28.20 ft) to the combined length of the nave and altar recess (57.05 ft) is 1:2, with a discrepancy of 1.1%. The total interior length of the church, from the east wall behind the altar to the west wall of the narthex, is 67.05 ft. The ratio of this length to the nave width between side pilasters is 4:3, to 1.3%.
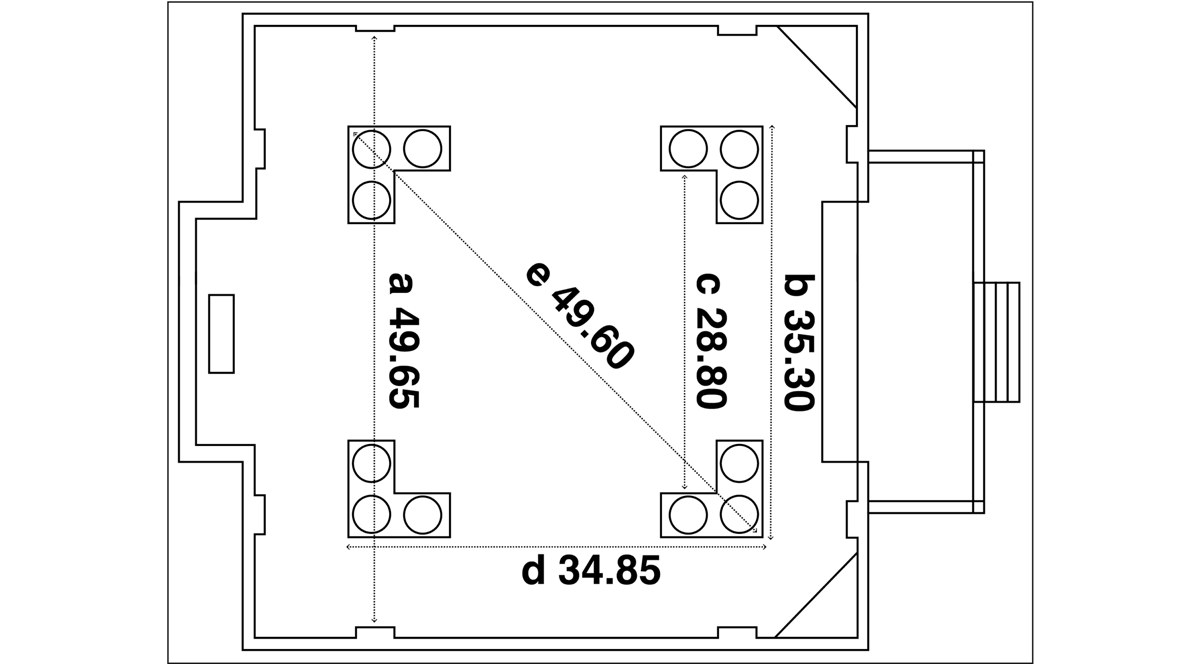
Within the square of the nave lies a smaller square, defined by the colonnades of giant Corinthian columns that support the main entablature (Figure 16). The width across the nave between the outer edges of the colonnade pedestals is 35.30 ft. Multiplied by √2, this matches the nave width between pilasters, with a discrepancy of 0.5%. The width between the inner edges of the pedestals is 28.80 ft. Multiplied by √3, this again matches the nave width between pilasters, to 0.5%. The length along the nave between the outer edges of the column pedestals is 34.85 ft. If an imaginary rectangle were to be constructed, with a length of 34.85 ft and a width of 35.30 ft, then the diagonal of the rectangle would be 49.60 feet. This is a very close match with the nave width between pilasters (to 0.1%).
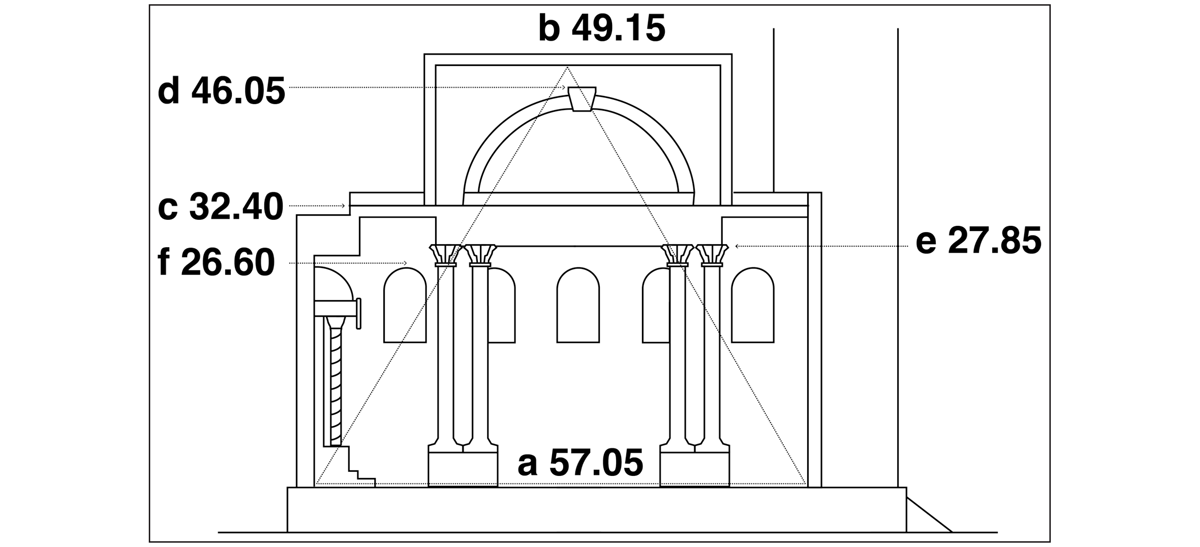
When investigating the vertical dimensions of the church, two triangular constructions were identified, similar to those at Christ Church. The combined length of the nave and altar recess is 57.05 ft (on the south side). If an imaginary equilateral triangle were to be constructed on this length, at nave floor level, then the height of the triangle would match the height of the nave ceiling (49.15 ft), with a discrepancy of 0.5%, some three inches (Figure 17). Pyramids and equilateral triangles were considered significant in masonic lore, since Freemasons considered the Egyptians to be the first true masons. If an equilateral triangle were to be constructed on the nave width between side pilasters, the height of the triangle would match the height to the bottom of the lunette window keystones (43.45 ft), with a discrepancy of 1.0% (Figure 18).
Keystones enlarged in a Mannerist fashion occur so frequently in Hawksmoor’s work that they are almost a defining characteristic. Here they seem to play a prominent role in the design scheme of the church (Figure 19). The height from the nave floor to the main order cornice (32.40 ft), when multiplied by √2, matches the height to the top of the lunette window keystones (46.05 ft), with a discrepancy of 0.5%. The ratio of the height of the main order architrave (27.85 ft) to the height to the top of the keystones is 3:5, to 0.8%. The north wall of the church is blank, but the south wall has windows (Figure 20). The height to the top of the windows (26.60 ft), when multiplied by √3, matches the height to the top of the keystones, almost exactly. Some other proportional relationships were found. The ratio of the height of the main order cornice to the height of the nave ceiling is 2:3, with a discrepancy of 1.1%. The ceiling of the side aisles outside the central square of the nave has a height of 31.20 ft. The ratio of this height to the nave length is 3:5, almost exactly. The ratio of the ceiling height to the nave width between side walls is again 3:5, with a discrepancy here of 0.2%. Finally, the chancel arch at the east end frames the altar and reredos. The height from the nave floor to the soffit of the arch is 26.00 ft. The ratio of this height to the height of the main order cornice (32.40 ft) is 4:5, with a discrepancy of 0.3%. These proportional relationships found at St Mary Woolnoth are summarised in Table 2 below.
St Mary Woolnoth, the nave looking towards the south wall, showing the windows, the main architrave, and the side aisle ceiling. The south-east side pilaster is to the left. The woodwork remaining from the now removed south gallery can be seen, and the south-west colonnade pedestal (bottom right). Photo: Jonathan Hales, 2023.
The proportional ratios tabulated above suggest a sequence of steps by which Hawksmoor may have evolved his design at St Mary Woolnoth. He was clearly intending a fundamentally cubic design, within the constraints of the existing site. The nave width between the side walls closely matches the length of the nave, up to the altar recess. The nave length could have generated the height of the side aisle ceiling (5:3). The combined length of the nave and altar recess could have determined the height of the nave ceiling (by triangulation), and also the width of the narthex (2:1). The total interior length of the church could have generated (4:3) the nave width between the side pilasters (which could also have been derived from the height of the nave ceiling). In turn, the nave width between pilasters could have determined the placement and dimensions of the four colonnade pedestals. It could also have generated (by triangulation) the height to the bottom of the lunette window keystones. The height of the nave ceiling could have given (3:2) the height of the main order cornice, which in turn could have determined the height of the lunette window keystones (1:√2). The keystones could have generated the height of the main architrave (3:5) and the height of the south aisle windows (1:√3). Finally, the height of the main order cornice could have given the height of the chancel arch (5:4).
Discussion: Hawksmoor’s Choice of Design Ratios
In a study such as this, it is always possible to argue that the correspondences that were identified between the measured dimensions of a building and hypothesised design ratios are coincidental. Indeed, if there were only a few such matches, this would be a valid objection, particularly if the matches had a large discrepancy. However, the significant number of matches (34) found across the two churches, and the small degrees of discrepancy, make it hard to sustain this argument. There are only five matches with a discrepancy of more than 1.0%; the majority have a discrepancy of 0.6% or less, in a context where the construction tolerance for proportional relationships across the two churches has been calculated as 0.4%. Only one of the potential matches that were identified goes beyond 1.4% (this being the diagonal of the nave rectangle at Christ Church). The possibility of all these correspondences being coincidental is statistically very small indeed.
This makes a strong case that Hawksmoor made the decision at both Christ Church and St Mary Woolnoth to use the design ratios and procedures that he associated with Gothic building. He did this perhaps as a reference to the English medieval parish church tradition. This association was likely reinforced by his contact with Freemasonry, with its celebration of the medieval masons and its iconography of cubes and pyramids, squares and triangles. It is also possible that geometric design procedures and proportional ratios survived into the 18th century as an oral tradition among masons and builders. It may be no coincidence that Palladio and Borromini, who both used geometric proportions significantly more than their respective contemporaries, were apprenticed as stonemasons before they became architects (Hales 2020; Hales 2023). There is also the possibility that Hawksmoor was influenced by Wren. There are some indications that Wren on occasion used geometric ratios, but at present there is little detailed evidence.20 This would be a fruitful area for some further survey-based research.
Conclusion
The detailed survey measurements at Christ Church and St Mary Woolnoth, and the proportional relationships that have been deduced from them, make a strong case that Hawksmoor was making conscious and deliberate use of the combination of whole-number and geometric ratios that he most likely associated with medieval Gothic building. The square constructions identified at St Mary Woolnoth and the rectangular constructions found at Christ Church suggest that Hawksmoor was emulating medieval design ad quadratum. The triangular constructions found in both churches seem to follow design ad triangulum. Establishing the proportional ratios present in both the horizontal and vertical dimensions at the churches has made it possible to suggest a series of steps by which Hawksmoor may have generated his design at each church. This study provides an interesting example of the design strategies common in the Middle Ages remaining relevant in 18th-century Britain. It raises questions about whether Hawksmoor used similar proportions in his other London churches, and whether such procedures were unique to him, or whether they were shared to any extent by his contemporaries.
Notes
- Hawksmoor also co-designed or contributed to two churches by John James. [^]
- They made this association despite the fact that the pointed arch first appeared (in Europe) in France, in the region around Paris, and it spread from there through France and England. Hawksmoor, following Wren, considered it was an import from Muslim (‘Saracen’) architecture in the Middle East (Hart 2002; Hart 2020). [^]
- In 1734, Langley wrote a public defence of Hawksmoor’s Stepney churches, including Christ Church, in the Grub Street Journal, following their condemnation by Palladian critic James Ralph (Hart 2002: 101, 181–85). [^]
- They were completed under John James in 1745. [^]
- Several of Wren’s City Churches were built or renovated with Gothic spires, pinnacles, or pointed windows: for example, St Alban Wood Street, St Mary Somerset, St Mary Aldermary, and St Dunstan-in-the-East (Hart 2020: 46–47). [^]
- An example being the Kitchen Court at Blenheim, with its mixture of castellated walls and classical pediments. [^]
- The letter is published in full in Downes (1959: 255–58). [^]
- The pentagon and the octagon were also sometimes used (see Hiscock 2007; Bork 2011; Murray 1989). [^]
- For more about medieval design based on square proportions, see the recent essays collected in Nancy Wu’s volume, Ad Quadratum (Wu 2002). [^]
- By the 18th century, these medieval approximations would not have been necessary. Professionals with some mathematical training were able to calculate such ratios using decimal notation, which had been introduced by James Napier in 1614. [^]
- Indeed, Borromini’s singular architecture was considered by many of his contemporaries to be a reversion to the Gothic style (see Wittkower 1974: 88–89). [^]
- It is more common to measure from the centre to the centre of columns. However, Matthew Cohen, in surveying Brunelleschi’s Basilica of San Lorenzo in Florence, found that the centre to centre measurement proved insignificant, while measuring to the inner edges of the column plinths revealed a proportional relationship of 1:√2 with the column heights (Cohen: 2013: 53–59). [^]
- This was a requirement stipulated by the Commission for Fifty New Churches. [^]
- Matthew Cohen writes that ‘proportional systems are executed in terms of local units of measurement’; hence to deduce the design scheme used in a building, it is necessary to translate survey measurements into the units of measurement used at the time the building was constructed (Cohen 2018: 530). [^]
- Several of these clergymen either sat on or else advised the Parliamentary Commission to Build Fifty New Churches (Du Prey 2000: 23–41). [^]
- Wren and Hawksmoor may have been influenced by the galleries at Hagia Sophia, illustrated in contemporary travel books (Downes 1982: 62; Hart 2002: 37). [^]
- The same arrangement had previously been used by Wren in his church of St. James, Piccadilly (1672–84), of which Wren was particularly proud (see Downes 1982: 53; Summerson 1953: 91). [^]
- Unpublished survey work by Jonathan Hales. [^]
- Hart discusses a list of Freemason Lodges active in 1730 that shows one ‘Nicholas Hawkesmore, Esq.’ as a prominent member of the Lodge meeting in Ludgate Street, near St Paul’s Cathedral (Hart 2002: 98). Hart notes that ‘Esquire’ implies particular eminence. [^]
- My recent (unpublished) survey at Wren’s St Stephen Walbrook found that the ratio of the height of the main east window (34.65 ft) to the nave width (60.10 ft) is 1:√3, with a discrepancy of just 0.1%. The height to the top of the dome at the lantern opening, which is 58.95 ft (and not, as claimed in several publications, 63 ft), forms the ratio 1:√2 with the nave length (83.30 ft), with again a discrepancy of only 0.1%. As a mathematician, Wren would have used √3 to calculate the curve of the cubic parabola incorporated in his drawing of around 1690 for the dome at St Paul’s (Higgott 2009). [^]
Author’s Note
I would like express my gratitude, for their kind assistance with this research, to Natasha Grimmett and Rachel Jamieson at Christ Church, Spitalfields; Inger Lannero at Lombard Churches; Colleen Goldspink and Stef Dickers at the Bishopsgate Institute Library; and all their respective staff teams. I also thank Liv White at Dopple Press for her help with the line drawings.
Competing Interests
The author has no competing interests to declare.
References
Ackerman, J. 1949. ‘Ars sine scientia nihil est’. Art Bulletin, 31(2): 81–111. DOI: http://doi.org/10.2307/3047224
Alberti, Leon Battista. 1988. On the Art of Building in Ten Books. Trans. by J. Rykwert, N. Leach, R. Tavernor. Cambridge, MA, and London: The MIT Press.
Barnes, C. 2009.The Portfolio of Villard de Honnecourt: A New Critical Edition and Color Facsimile. Farnham: Ashgate.
Bork, R. 2011.The Geometry of Creation: Architectural Drawing and the Dynamics of Gothic Design. Abingdon, Oxon and New York: Ashgate.
Bork, R. 2014. The Geometry of Bourges Cathedral. Architectural Histories, 2(1): 24, 1–4. DOI: http://doi.org/10.5334/ah.bz
Cohen, M. 2013. Beyond Beauty: Reexamining Architectural Proportion through the Basilicas of San Lorenzo and Santo Spirito in Florence. Venice: CISA/Marsilio.
Cohen, M. 2018. Ten Principles for the Study of Proportional Systems in the History of Architecture. In: Cohen, M, and Delbeke, M (eds.), Proportional Systems in the History of Architecture: A Critical Reconsideration, 525–550. Leiden: Leiden University Press.
Coldstream, N. 2002. Medieval Architecture. Oxford: Oxford University Press.
Downes, K. 1959. Hawksmoor. London: A. Zwemmer.
Downes, K. 1982. The Architecture of Wren. London: Granada Publishing.
Du Prey, P. 2000. Hawksmoor’s London Churches: Architecture and Theology. Chicago and London: University of Chicago Press.
Fletcher, R. 2019. Geometric Proportions in Measured Plans of the Pantheon of Rome. Nexus Network Journal 21: 83–106. DOI: http://doi.org/10.1007/s00004-018-00423-2
Hales, J. 2020. Baroque constructive geometry? Borromini’s design for the elevation at San Carlino. In: Mansure, A, and Laurasi, S (eds.) Finding San Carlino: Collected Perspectives on the Geometry of the Baroque, 73–85. London and New York: Routledge. DOI: http://doi.org/10.4324/9780429457876-6
Hales, J. 2023. Proportion and Ratio in Palladio’s Redentore. Nexus Network Journal, 25(1): 83–106. DOI: http://doi.org/10.1007/s00004-022-00641-9
Hallier, G. 1990. La geometrie des amphitheatres militaires sur les limes du Rhin et du Danube. In: Akten des 14. Internationalen Limeskongresses in Carnuntum (con. Vienna 1986), 71–82.
Harrison, D. 2009. The Genesis of Freemasonry. Hersham, Surrey: Lewis Masonic/Ian Allan.
Hart, V. 2002. Nicholas Hawksmoor: Rebuilding Ancient Wonders. New Haven and London: Yale University Press.
Hart, V. 2008. Sir John Vanbrugh: Storyteller in Stone. New Haven and London: Yale University Press.
Hart, V. 2020. Christopher Wren: In Search of Eastern Antiquity. New Haven and London: Yale University Press.
Higgott, G. 2009. Geometry and Structure in the Dome of St Paul’s. In: Gerbino, A and Johnston, S (eds.), Compass and Rule: Architecture as Mathematical Practice in England 1500–1750, 154–169. New Haven and London: Yale University Press.
Hiscock, N. 2000. The Wise Master Builder: Platonic Geometry in Plans of Medieval Abbeys and Cathedrals. Abingdon, Oxon. and New York: Ashgate.
Hiscock, N. 2007. The Symbol at Your Door: Number and Geometry in Religious Architecture of the Greek and Latin Middle Ages. Aldershot: Ashgate.
Hopkins, O. 2015. From The Shadows: The Architecture and Afterlife of Nicholas Hawksmoor. London: Reaktion Books.
Jacobson, D. 1990. The Plan of Herod’s Temple. Bulletin of the Anglo-Israel Archaeological Society, 10: 36–66.
Kalayan, H. 1971. The Temple of Bacchus and its Geometry of Proportion and Symmetry. Bulletin du Musee de Beyrouth, 24: 157–65.
Kidson, P. 1990. A Metrological Investigation. Journal of the Warburg and Courtauld Institutes, 53: 71–97. DOI: http://doi.org/10.2307/751340
Kidson, P. 2008. Roriczer’s Iceberg. Journal of the Warburg and Courtauld Institutes, 71: 1–20. DOI: http://doi.org/10.1086/JWCI20462773
Langley, B. 1726. Practical Geometry Applied to the Useful Arts of Building, Surveying, Gardening, and Mensuration. London: John Millan.
Langley, B, and Langley, T. 1742. Ancient Architecture Restored Retitled 1747: Gothic Architecture, Improved by Rules and Proportions. London: John Millan.
Mitrović, B. 2004. Learning from Palladio. New York and London: W.W. Norton & Company.
Murray, S. 2014. Plotting Gothic: A Paradox. Architectural Histories, 2(1): 16, 1–22. DOI: http://doi.org/10.5334/ah.bs
Murray, S. 2015. Plotting Gothic. Chicago: University of Chicago Press. DOI: http://doi.org/10.7208/chicago/9780226191942.001.0001
Napier, J. 1614. Mirifici logarithmorum canonis descriptio. Edinburgh: Andrew Hart.
Palladio, A. 1997. The Four Books on Architecture. Trans. by R Tavernor and R Schofield. Cambridge, MA and London: MIT Press.
Sandron, D, and Tallon, A. 2013 Notre-Dame de Paris: Neuf Siecles d’Histoire Paris: Parisgramme.
Serlio, S. 1996. Sebastiano Serlio on Architecture, Volume One: Books I –V of Tutte L’Opere d’Architettura e Prospetiva. Trans. by V Hart and P Hicks. New Haven and London: Yale University Press.
Shelby, L. 1972. The Geometrical Knowledge of Mediaeval Master Masons. Speculum, 47(3): 395–421. DOI: http://doi.org/10.2307/2856152
Shelby, L. 1976. Gothic Design Techniques. Carbondale: Southern Illinois University Press.
Sheppard, F (ed.). 1957. Survey of London; Volume 27: Spitalfields and Mile End New Town. London: London County Council. Digitised and sponsored by English Heritage, British History Online.
Summerson, J. 1953. Sir Christopher Wren. London: Collins.
Wilson Jones, M. 2003. Principles of Roman Architecture. 2nd ed. New Haven and London: Yale University Press.
Wittkower, R. 1962. Architectural Principles in the Age of Humanism. 3rd ed. London: Alec Tiranti.
Wittkower, R. 1974. Gothic Versus Classic: Architectural Projects in Seventeenth Century Italy London: Thames and Hudson.
Wu, N (ed.). 2002. Ad Quadratum: The Practical Application of Geometry in Medieval Architecture. Abingdon, Oxon and New York: Ashgate.
Zenner, M-T. 2002. A Proposal for Constructing the Plan and Elevation of a Romanesque Church Using Three Measures. In: Wu, N (ed.), Ad Quadratum: The Practical Application of Geometry in Medieval Architecture, 25–55. Abingdon, Oxon and New York: Ashgate.